C2W2 优化算法

吴恩达深度学习C2W2 优化算法

1、mini-batch 梯度下降法

如果训练集较小（小于2000个样本），则直接使用 batch 梯度下降法（即 mini-batch size = m）
如果训练样本数据较大，mini-batch size 一般设为 64-512 ，设为 2 的 n 次方，代码运行快一些。也有设为 1024 的，比较少见

使用 batch 梯度下降法，一次遍历训练集只能做一个梯度下降；使用 mini-batch 梯度下降法，一次遍历训练集（1 epoch），能做 n 个梯度下降（n 为划分的 mini-batch 数目）

2、优化算法（加速梯度下降）

2.1、指数加权平均

$v_t = \beta v_{t-1} + (1-\beta)\theta_t$ $若 \theta 代表当日气温， v_t 可视为过去\frac{1}{1-\beta} 天温度的指数加权平均$

占用极少内存（只占用一行代码，且计算指数加权平均数也只占用当行数字的存储，只需要把最新数据代入公式，不断覆盖就可以）

偏差修正

当 β 值设的较大时（eg. 0,98)，初期估测值不准（过小），可以用 $\frac{v_t}{1 - \beta^t}$ 代替 $v_t$ 来估测第 t 天的温度值。

随着 t 的增大，$\beta^t$ 的值接近于 0 ，偏差修正几乎没有作用。

但如果你关心初始时期的偏差，在刚开始计算指数加权平均时，偏差修正能帮你在早期获取更好的估测。，使得指数加权平均数的运算更加准确（特别是在估测初期）。

2.2 （Momentum）动量梯度下降法

基本思想：计算梯度的指数加权平均数，并利用该梯度更新你的权重。

目的：加速梯度下降

1 2	On iteration t: # Compute dW,db on the current mini-batch

$v_{dw}, v_{db} 初始值为0，一般设 \beta = 0.9，\alpha需要调试$ $v_{dw} = \beta v_{dw} + (1 - \beta) dW$ $v_{db} = \beta v_{db} + (1 - \beta) db$ $W = W - \alpha v_{dW}, b = b - \alpha v_{db}$

有2个超参数，α 和 β。β 的值常设为0.9，这相当于平均了前10次迭代的梯度，而10次迭代后已过了初始阶段，所以不需要偏差修正。

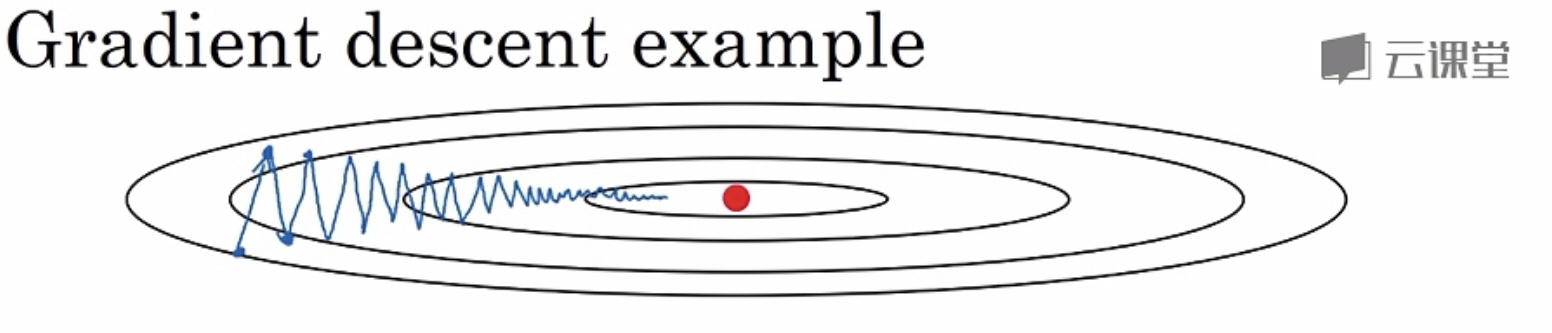
原理：通过以上的公式计算加权平均，结合下面的图：

在纵轴（偏置b）方向，平均的过程中，正负相抵，所以接近于0，所以用指数加权平均数更新偏置b，在纵轴方向波动减小。
在横轴（权重W）方向，由于所有微分都指向横轴方向，所以平均值仍较大，所以用指数加权平均数更新权重W，在横轴方向依旧有更快的学习速度

2.3 RMSprop算法（均方根算法）

目的：加速梯度下降

RMSprop和Momentum有很相似的一点，可以消除梯度下降中的摆动，并允许你使用一个更大的学习率α，从而加快你的学习算法速度。

1 2	On iteration t: # Compute dW,db on the current mini-batch

$S_{dw}, S_{db} 初始值为0，一般设 \beta = 0.999，\alpha需要调试$ $S_{dW} = \beta S_{dW} + (1 - \beta) (dW)^2$ $S_{db} = \beta S_{db} + (1 - \beta) (db)^2$ $W:= W - \alpha \frac{dW}{\sqrt{S_{dW}}}, b := b - \alpha \frac{db}{\sqrt{S_{db}}}$

原理：因为db较大，dW较小（可以从2.2的图看出纵轴的倾斜程度大，所以b的梯度db大）；所以$S{db}$也较大，而$S{dW}$则较小；所以相当于在更新时b的学习率较小，而W的学习率较大；这就达到了消除纵向摆动，加快横向更新速度的目的。

不过为了保证在更新参数时不会出现除以0的情况，最后一步的更新操作通常更改为：

$W:= W - \alpha \frac{dW}{\sqrt{S_{dW}} + \varepsilon}, b := b - \alpha \frac{db}{\sqrt{S_{db}} + \varepsilon}$

2.4 Adam算法

基本思想：结合 Momentum 和 RMSprop 。

1	Adam optimization algorithm

0初始化：

$V_{dW} = 0, S_{dW} = 0, V_{db} = 0, S_{db} = 0$

1 2	On iteration t: # Compute dW,db on the current mini-batch

计算Momentum指数加权平均：

$v_{dw} = \beta_1 v_{dw} + (1 - \beta_1) dW,v_{db} = \beta_1 v_{db} + (1 - \beta_1) db$

RMSprop：

$S_{dW} = \beta_2 S_{dW} + (1 - \beta_2) (dW)^2,S_{db} = \beta_2 S_{db} + (1 - \beta_2) (db)^2$

偏差修正：

$v_{dW}^{corrected}\frac{v_{dW}}{1 - \beta_1^t}, v_{db}^{corrected}\frac{v_{db}}{1 - \beta_1^t}$ $S_{dW}^{corrected}\frac{S_{dW}}{1 - \beta_2^t},S_{db}^{corrected}\frac{S_{db}}{1 - \beta_2^t}$

更新权重：

$W := W - \alpha \frac{v_{dW}^{corrected}}{\sqrt{S_{dW}^{corrected}} + \varepsilon}, b := b - \alpha \frac{v_{db}^{corrected}}{\sqrt{S_{db}^{corrected}} + \varepsilon}$

以上就是Adam算法，超参数缺省值如下：

$\alpha 需要调试，\beta_1 = 0.9，\beta_2 = 0.999，\varepsilon = 10^{-8}$

一般直接使用这些超参数的缺省值，不需要修改。

2.5 学习率衰减

基本思想：学习率随时间慢慢减少。在学习初期学习率较大，即有较大的更新步伐；当开始收敛时，学习率较小，即更新步伐较小。

几种学习率衰减模式：

$\alpha = \frac{1}{1 + decay\_rate * epoch\_num} \alpha_0$ $decay\_rate称为衰减率，epoch\_num为代数，\alpha_0为初始学习率$ $decay\_rate和\alpha_0是两个需要调整的超参数$
指数衰减：
$\alpha = 0.95^{epoch\_num} \alpha_0$
$\alpha = \frac{k}{\sqrt{epoch\_num}} \alpha_0$ $或者 \alpha = \frac{k}{\sqrt{t}} \alpha_0, t为mini-batch的序号$